Create an Equation and Sketch a Graph That is Linear is Continuous
Linear equation graphs
Jump to
Key points
-
Graphs of two or more straight lines can be used to solve simultaneous linear equations.
-
The graph of a straight line can be described using an .
- lines are written as \(y = c\)
- lines are written as \(x = c\)
- are written as \(y = mx + c\)
-
\(m\) is a number which is a measure of the steepness of the line. This is the .
-
\(c\) is the number where the line crosses the \(y\) -axis. This is the \(y\) .
-
The of the points on an oblique line are calculated by given values of \(x\) into the equation \(y = mx + c\)
Recognise and draw the lines 𝒚 = 𝒙 and 𝒚 = -𝒙
All the points on the line \(y = x\) have coordinates with equal values for \(x\) and \(y\)
- To draw the line \(y = x\) :
- Plot points with coordinates where \(x\) and \(y\) are equal. Three points are sufficient, but more can be plotted.
- Draw a line through the plotted points.
All the points on the line \(y = -x\) have coordinates with values for \(x\) and \(y\) that are equal in but with opposite signs.
If \(x\) is positive, \(y\) is negative. If \(x\) is negative, \(y\) is positive.
- To draw the line \(y = -x\) :
- Plot points with coordinates where \(x\) and \(y\) have equal magnitude but opposite signs.
- Draw a line through the plotted points.
Examples

The straight line 𝒚 = 𝒙 passes through the origin. All the points on the line 𝒚 = 𝒙 have coordinates with equal values for 𝒙 and 𝒚
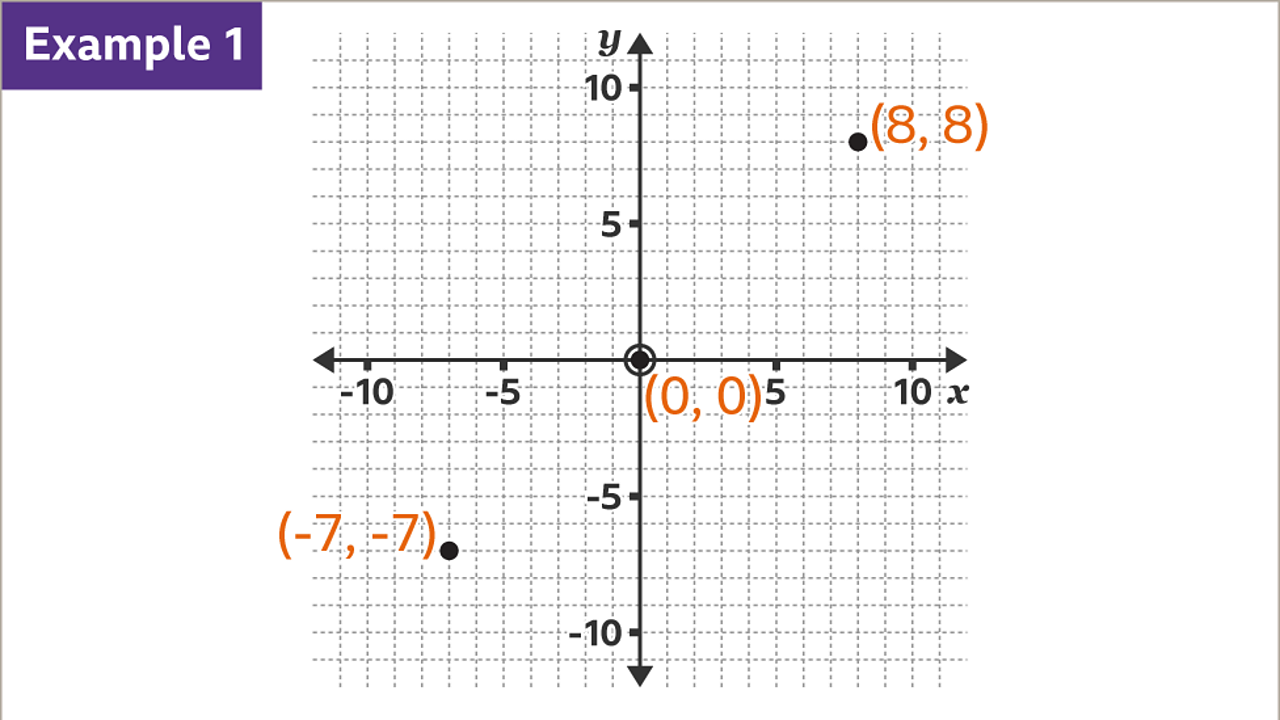
To draw the line 𝒚 = 𝒙, plot points with coordinates where 𝒙 and 𝒚 are equal. Although three points are sufficient, more points may be plotted. Using well-spaced points, such as the coordinates (-7, -7), (0, 0) and (8, 8), the line may be accurately drawn.
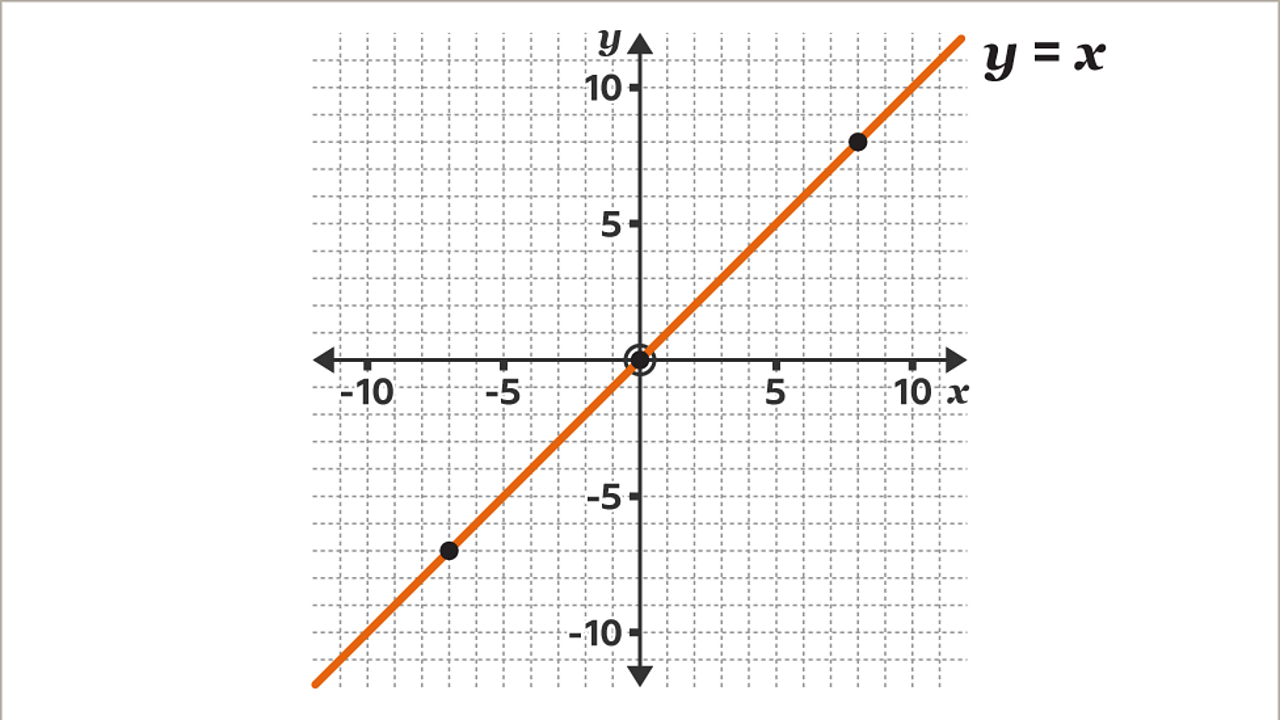
Next, draw a line through the plotted points. Label the line 𝒚 = 𝒙. The scales on the axes are equal, 𝒚 = 𝒙 is a diagonal line passing through the origin.
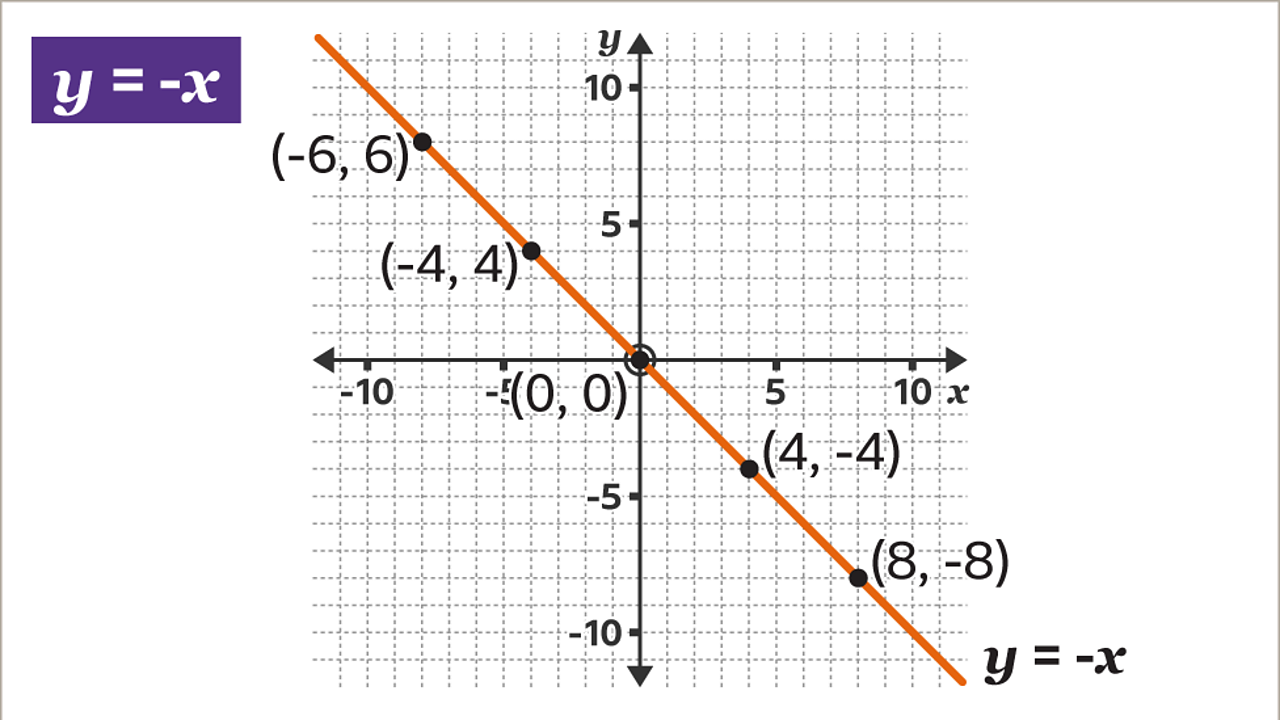
The straight line, 𝒚 = -𝒙 passes through the origin. All the points on the line 𝒚 = -𝒙 have coordinates with values for 𝒙 and 𝒚 that are equal in magnitude but with opposite signs. If 𝒙 is positive, 𝒚 is negative. If 𝒙 is negative, 𝒚 is positive.
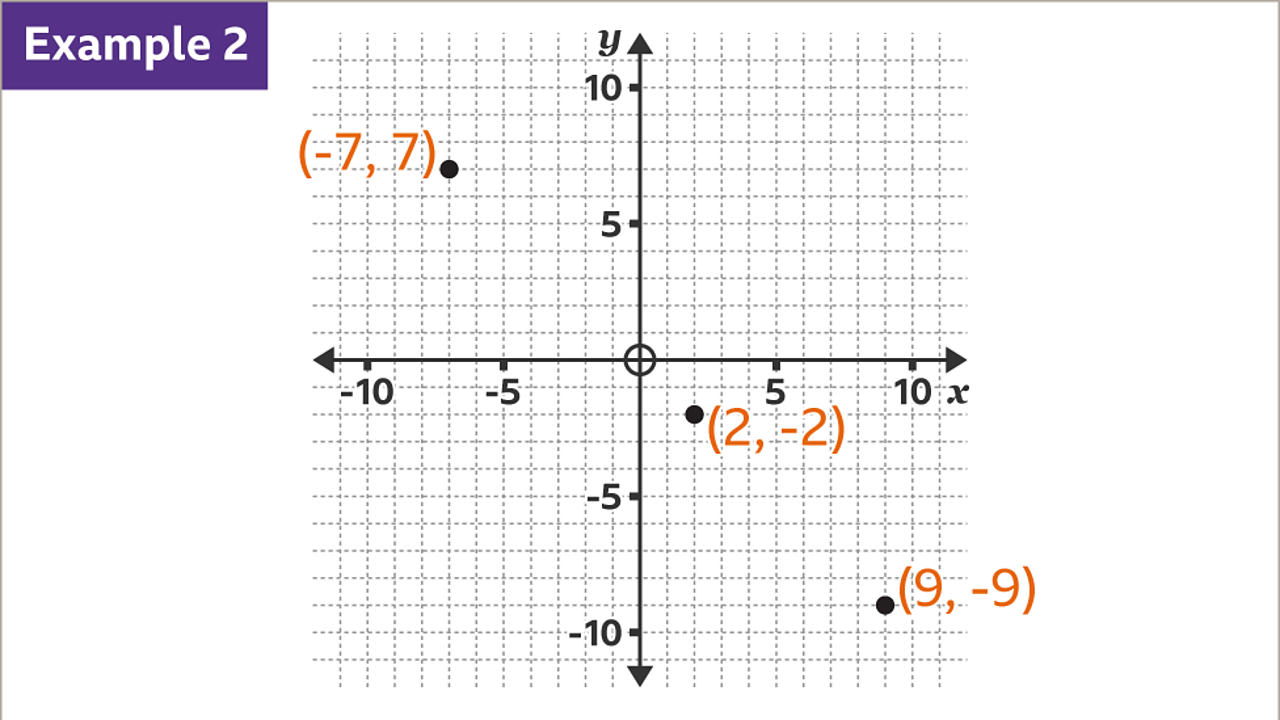
To draw the line 𝒚 = -𝒙, plot points with coordinates where 𝒙 and 𝒚 have equal magnitude but opposite signs. For example, the coordinates (-7, 7), (2, -2) and (9, -9) have 𝒙 and 𝒚 values that are equal in size, but with opposite signs, one being positive and the other negative.
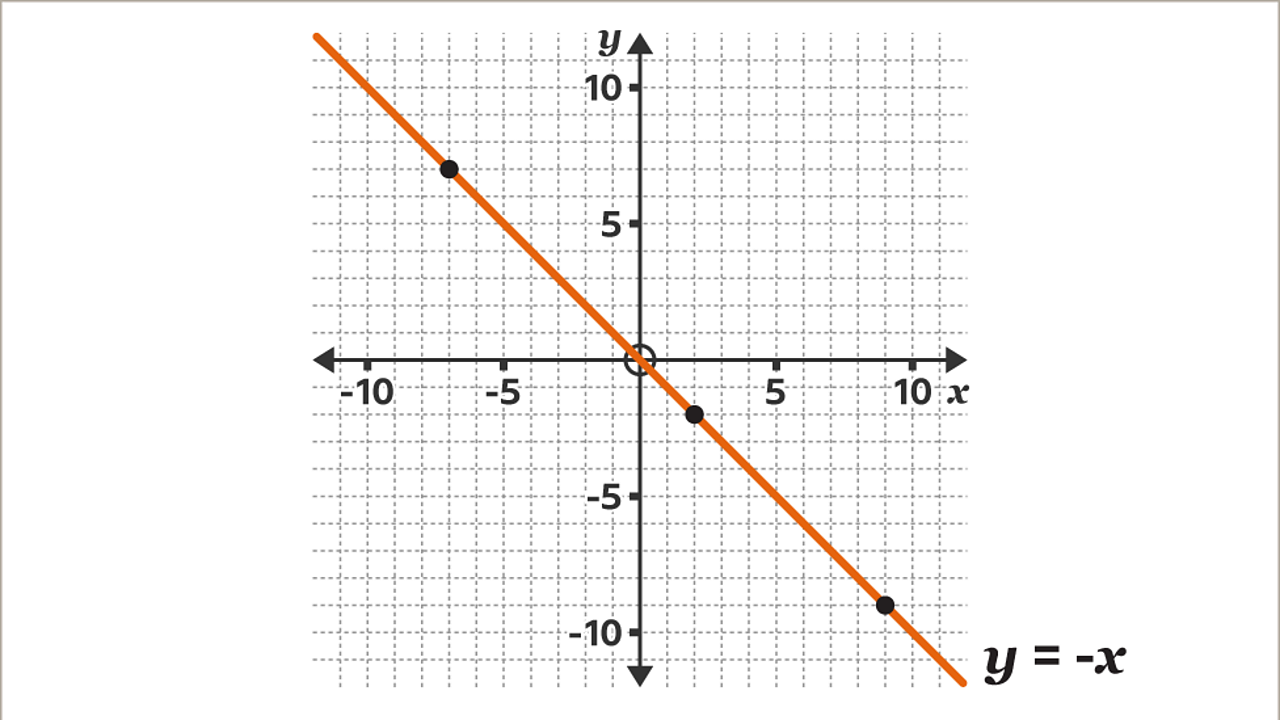
Draw a line through the plotted points. Label the line 𝒚 = -𝒙. The scales on the axes are equal, 𝒚 = -𝒙 is a diagonal line passing through the origin.
Question
Draw the graph 𝒚 = 𝒎𝒙 + 𝒄 by creating a table of values
\(m\) is a number which measures the steepness of the line. This is known as the gradient .
\(c\) is the number where the line crosses the \(y\) -axis. This is the \(y\) -intercept .
- To draw a graph of \(y = mx + c\) for given values of \(x\) :
- Use the given values for \(x\) to draw a table of values for \(x\) and \(y\)
- each value of \(x\) into the equation to find the value of \(y\) . Each pair of values give a coordinate.
- Use the coordinates to decide on that will take all the values of \(x\) and \(y\)
- Plot the coordinates and draw a line through the points. Label the line with the equation.
Example
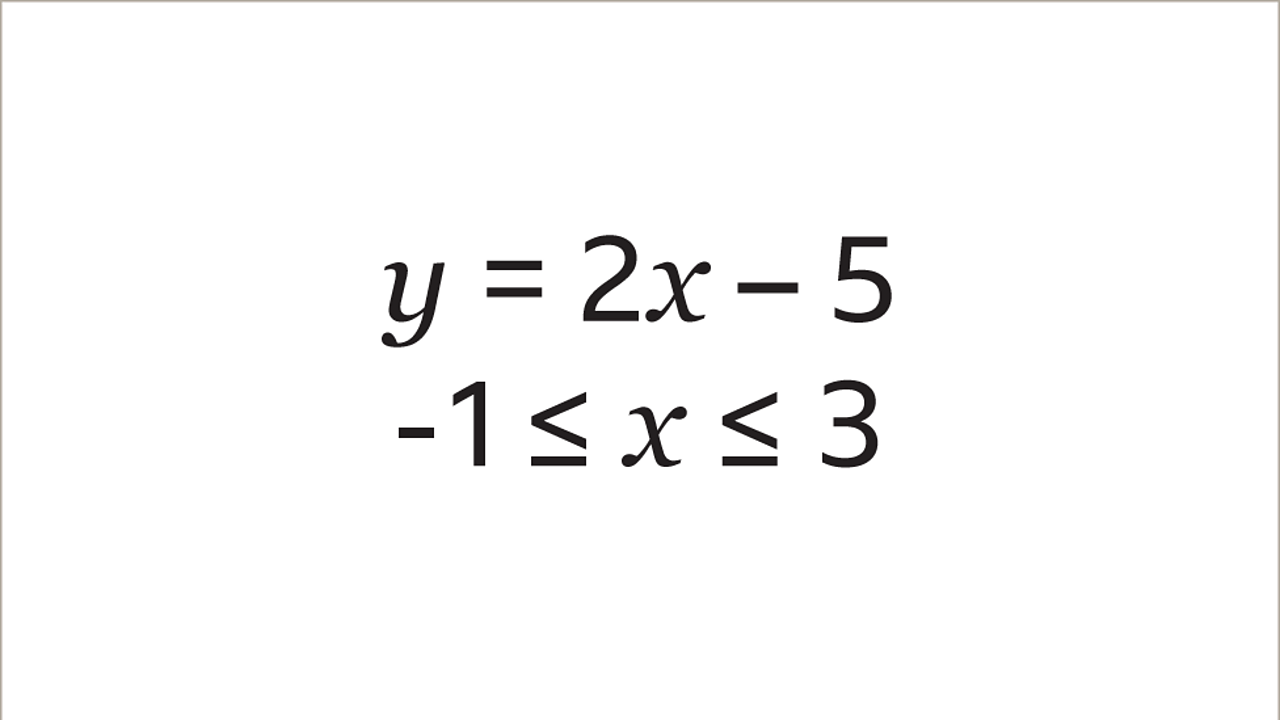
Draw the graph of 𝒚 = 2𝒙 – 5 for values of 𝒙 from -1 to 3. This is written as the inequality -1 ≤ 𝒙 ≤ 3
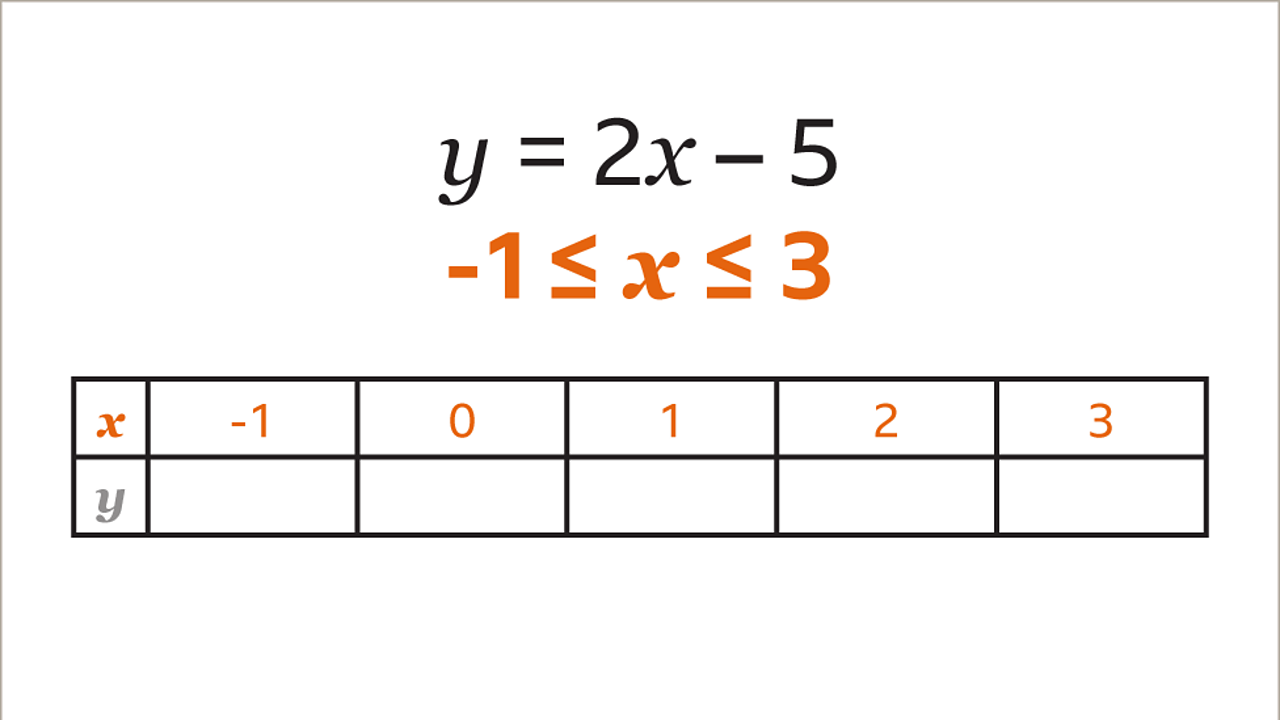
Use the given values for 𝒙 to draw a table for 𝒙 and 𝒚. -1 ≤ 𝒙 ≤ 3 means that the values of 𝒙 start at -1 and go up to 3
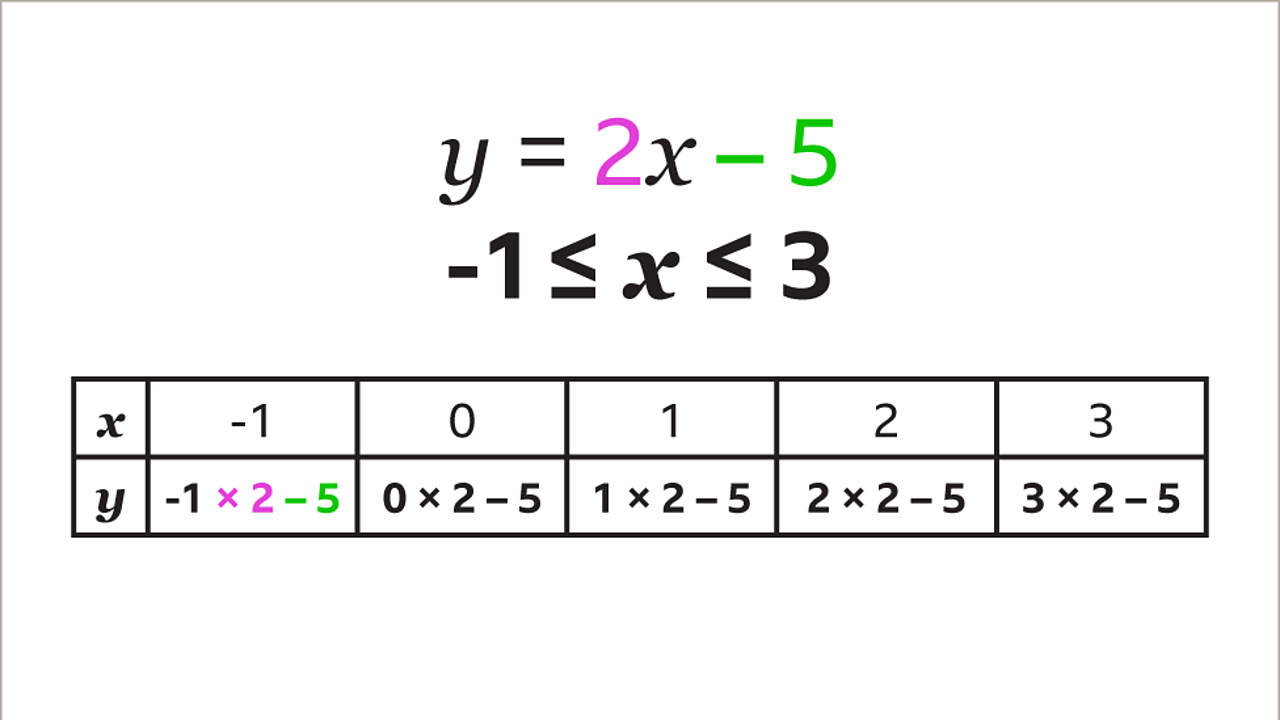
Substitute each value of 𝒙 into the equation 2𝒙 – 5 to find the value of 𝒚. 2𝒙 – 5 means that each value of 𝒙 is multiplied by 2 and then 5 is subtracted to give 𝒚. When 𝒙 = -1, the calculation to find 𝒚 is -1 × 2 – 5. The process is repeated for each value of 𝒙

Each calculation is evaluated to give 𝒚. When 𝒙 = -1 the calculation -1 × 2 – 5 gives 𝒚 = -7. When 𝒙 = 0 the calculation 0 × 2 – 5 gives 𝒚 = -5. Repeat this for each value of 𝒙
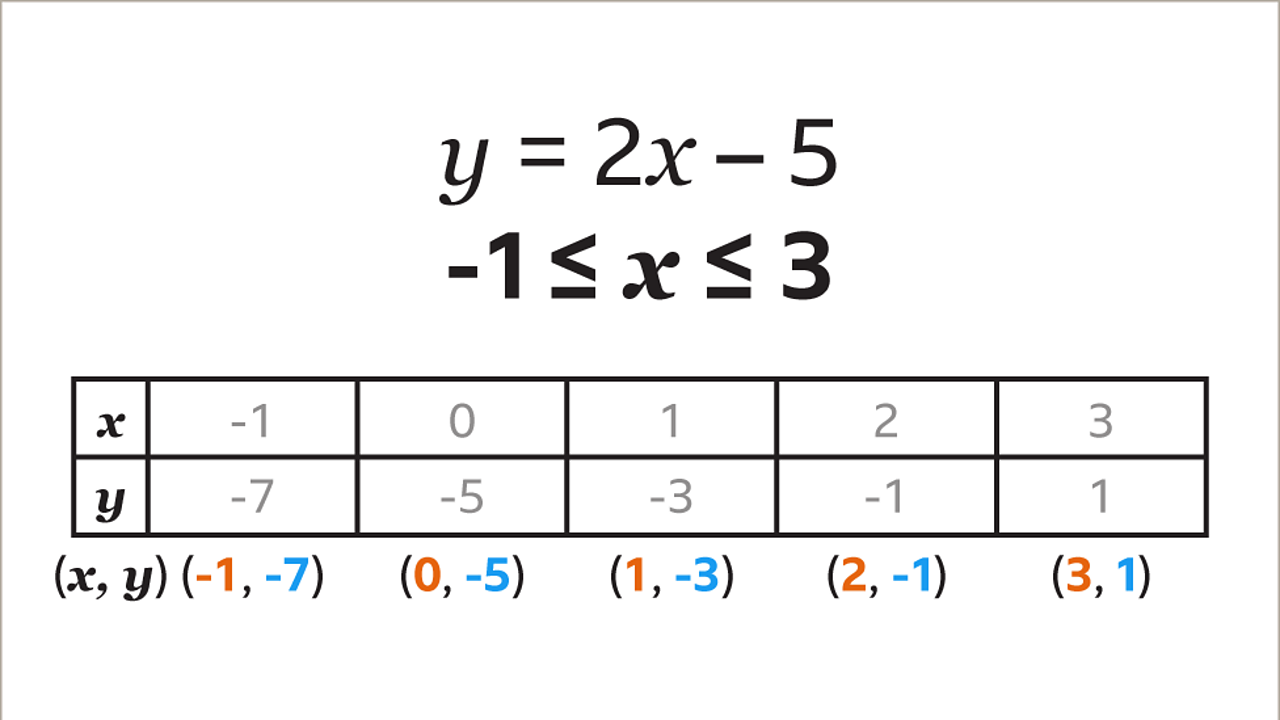
Use the pairs of values in the table to list the coordinates of the points to be plotted. The coordinates are (-1, -7), (0, -5), (1, -3), (2, -1) and (3, 1).

Use the coordinates to decide on axes that will take all the values of 𝒙 and 𝒚. The 𝒙-axis needs to include values from -1 to 3. This is shown as the inequality -1 ≤ 𝒙 ≤ 3. The 𝒚-axis needs to include values from -7 to 1. This is shown as the inequality -7 ≤ 𝒚 ≤ 1
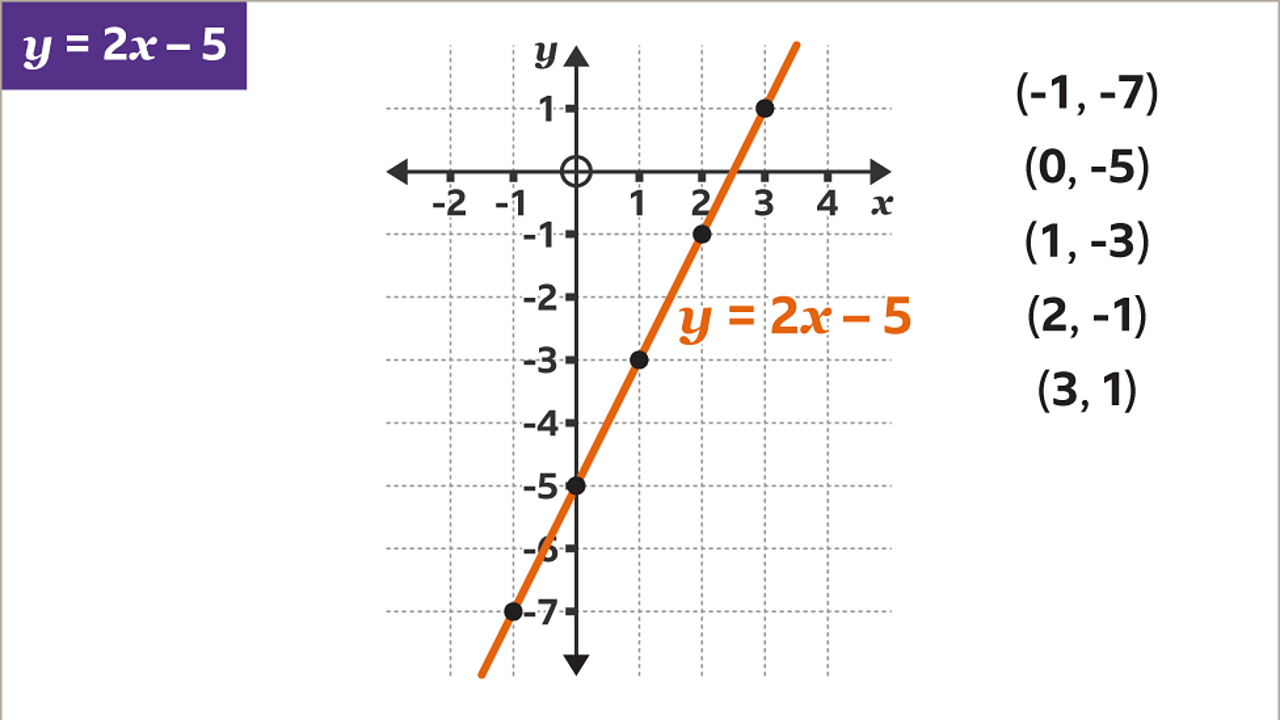
Plot the coordinates for 𝒚 = 2𝒙 – 5. Draw a line through the points and label the line.
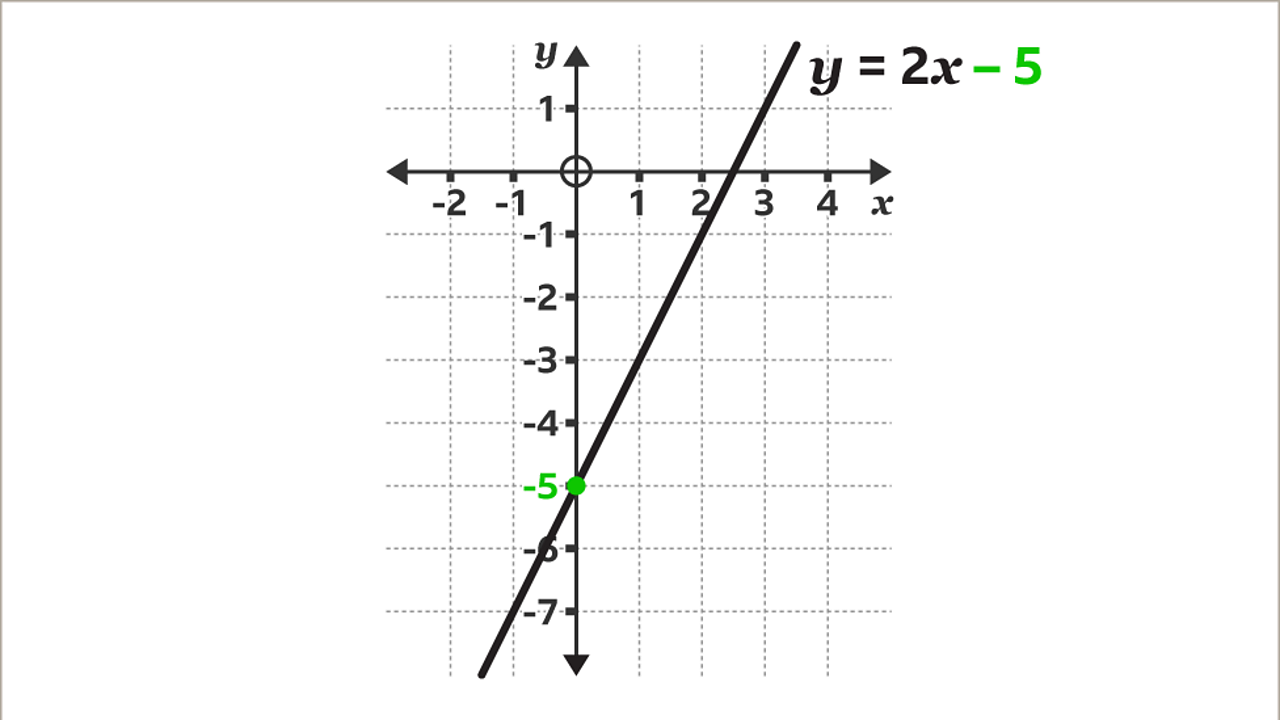
The 𝒚-intercept of the graph is -5. This is the constant (𝒄) in the equation 𝒚 = 2𝒙 – 5. The line crosses the 𝒚-axis at (0, -5).
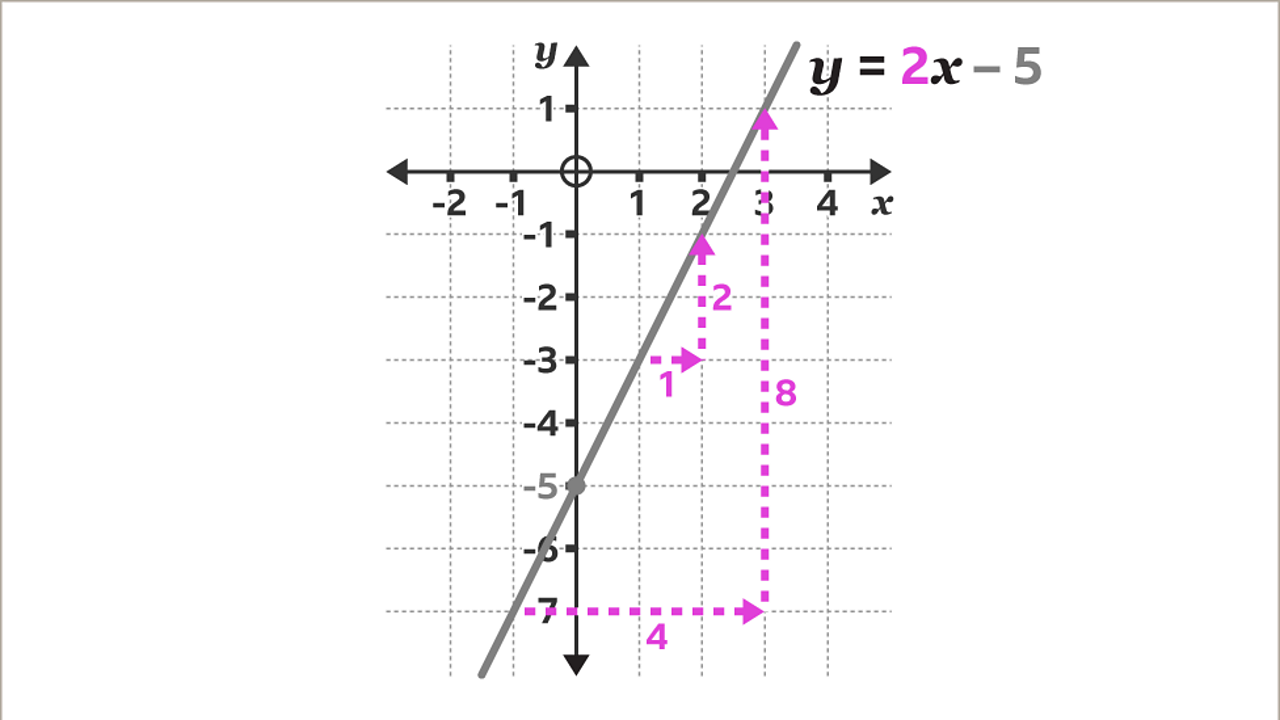
The gradient of the line 𝒚 = 2𝒙 – 5 is given by the coefficient of 𝒙 (2). For each one horizontal move to the right, the line moves vertically twice as much up. Eg, one horizontal unit to the right and two vertical units up. Similarly, four horizontal units to the right and eight vertical units up.
Questions
Reading 𝒙 and 𝒚 coordinates from a graph
A position on a graph is defined by coordinates ( \(x\) , \(y\) ). When one coordinate is given, the second can be read from the graph.
-
To find a \(y\) -coordinate from a given \(x\) -coordinate:
- On the \(x\) -axis, locate the given amount.
- Draw a vertical line, using a ruler, from the given amount up to the line.
- Draw a horizontal line, using a ruler, from the line across to the \(y\) -axis.
- Read the value on the \(y\) -axis.
-
To find an \(x\) -coordinate from a given \(y\) -coordinate:
- On the \(y\) -axis, locate the given amount.
- Draw a horizontal line, using a ruler, from the given amount across to the line.
- Draw a vertical line, using a ruler, from the line down to the \(x\) -axis.
- Read the value on the \(x\) -axis.
Examples
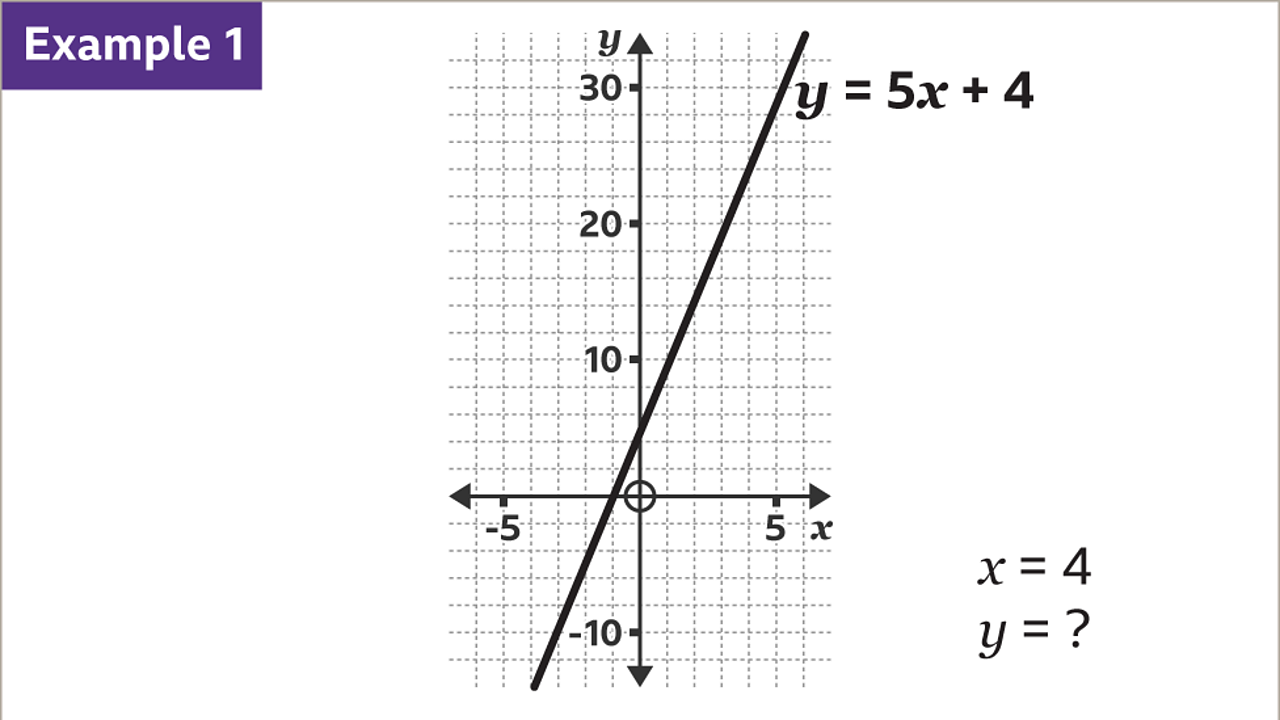
Use the graph to find the value of 𝒚 when 𝒙 = 4

On the 𝒙-axis, locate the given amount (4) and draw a vertical line, using a ruler, up to the line.
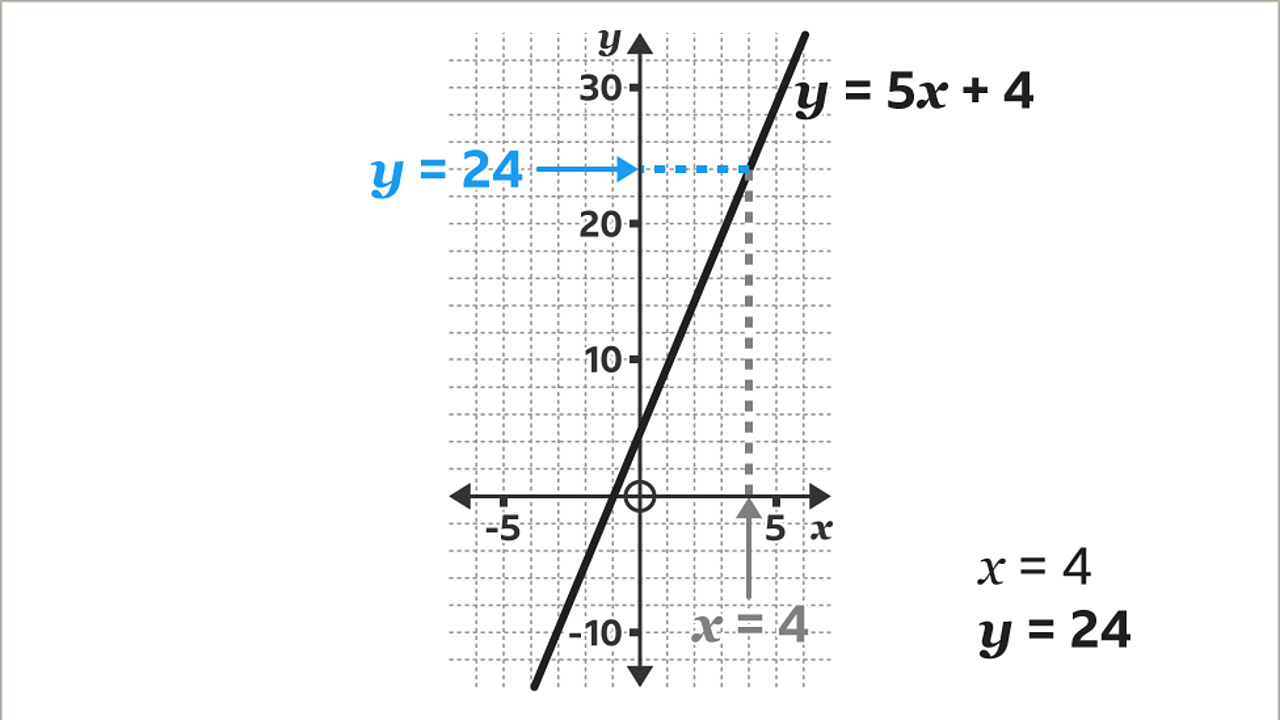
Then, draw a horizontal line, using a ruler, from the line across to the 𝒚-axis. Read the value on the 𝒚-axis. When 𝒙 = 4, 𝒚 = 24
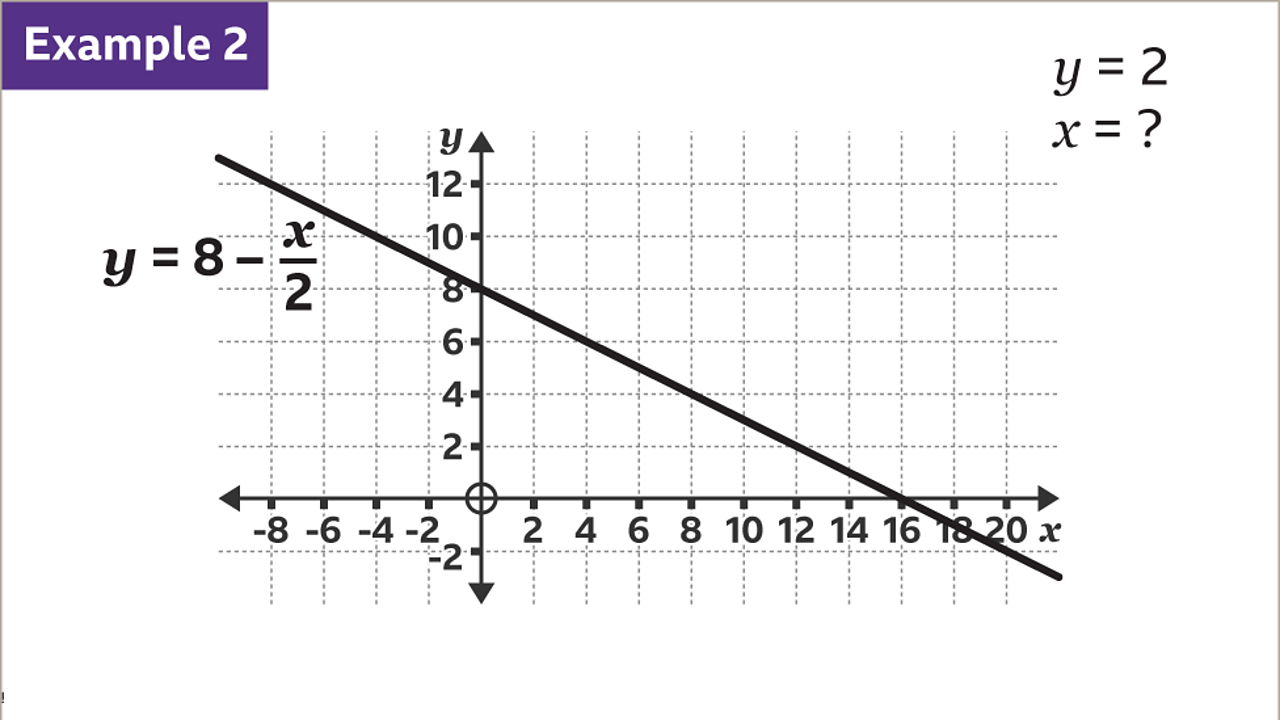
Use the graph to find the value of 𝒙 when 𝒚 = 2
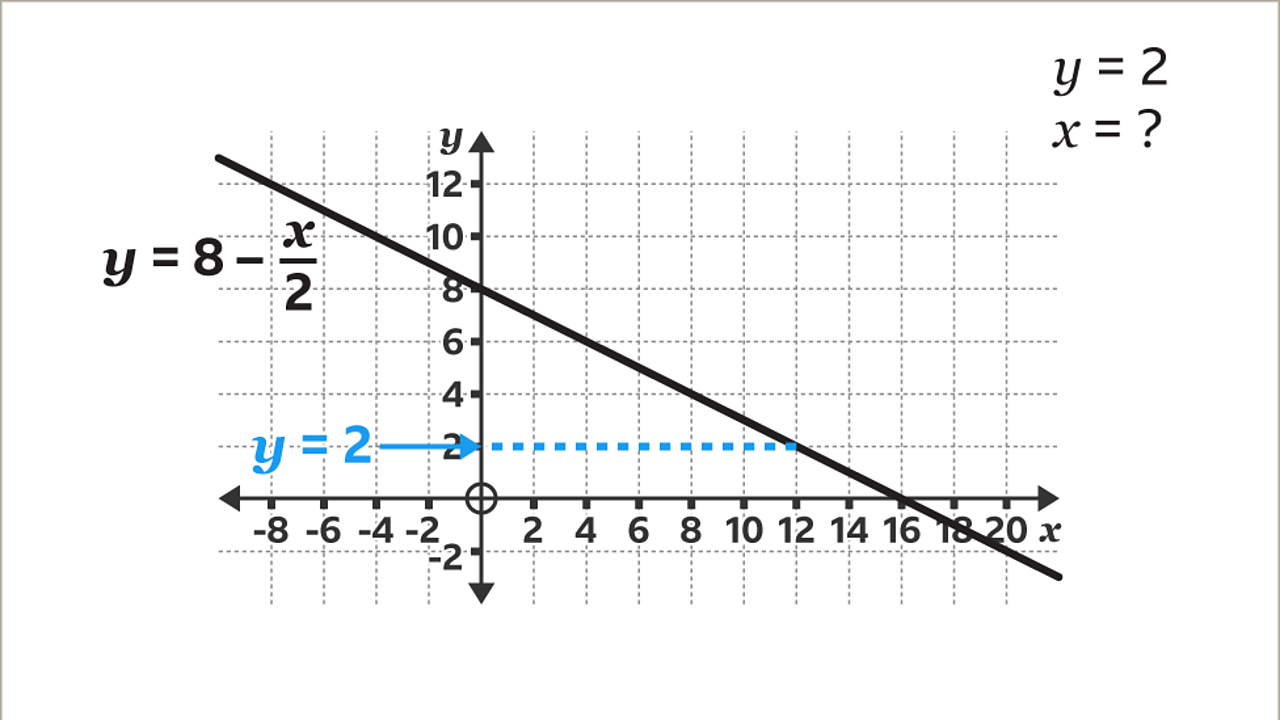
On the 𝒚-axis, locate the given amount (2) and draw a horizontal line, using a ruler, across to the line.
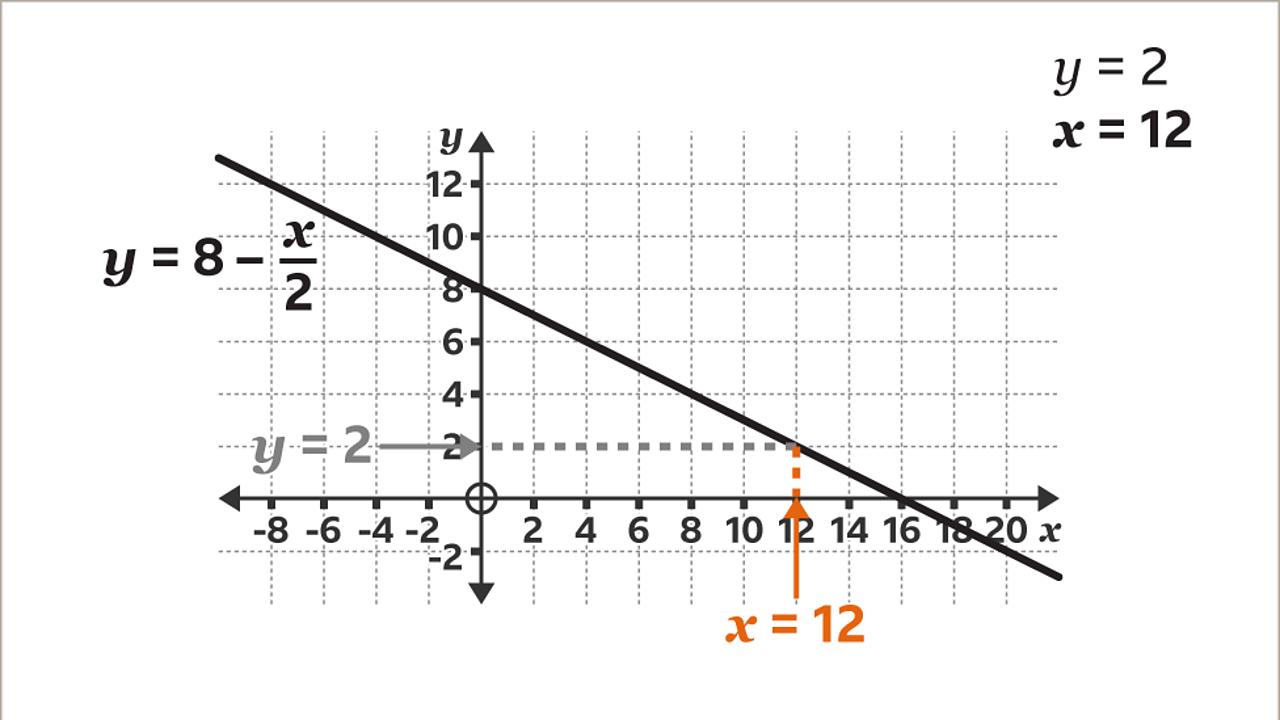
Draw a vertical line, using a ruler, from the line down to the 𝒙-axis. Read the value on the 𝒙-axis. When 𝒚 = 2, 𝒙 = 12
Question
Practise reading and plotting linear equation graphs
Quiz
Practise reading and plotting linear equation graphs with this quiz. You may need a pen and paper to help you.
Real-life maths
Linear graphs are commonly used when converting between different units of measurement.
For example, swapping between temperatures in degrees Celsius (°C) and degrees Fahrenheit (°F), exchanging between different currencies, such as pounds and euros, or changing inches into centimetres.
Linear graphs are useful to pharmacists and scientists in the pharmaceutical industry when working out the correct strength of drugs.
The amount of a drug for a given volume of medicine is critical, both for the medicine to be effective and for the safety of the patient.
Source: https://www.bbc.co.uk/bitesize/topics/zdbc87h/articles/zkpj2nb
0 Response to "Create an Equation and Sketch a Graph That is Linear is Continuous"
Post a Comment